득이공간
[백준 C++] 9465 스티커 - 다이나믹프로그래밍 본문
9465번: 스티커
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스의 첫째 줄에는 n (1 ≤ n ≤ 100,000)이 주어진다. 다음 두 줄에는 n개의 정수가 주어지며, 각 정수는 그 위치에 해당하는 스티커의
www.acmicpc.net

#include <iostream>
using namespace std;
int ST[2][100000];
int DP[2][100000];
void Test()
{
int N;
cin >> N;
for (int i = 0; i < 2; ++i)
{
for (int j = 0; j < N; ++j)
{
cin >> ST[i][j];
}
}
if (N <= 1)
{
cout << max(ST[0][0], ST[1][0]) << '\n';
return;
}
DP[0][0] = ST[0][0];
DP[1][0] = ST[1][0];
DP[0][1] = DP[1][0] + ST[0][1];
DP[1][1] = DP[0][0] + ST[1][1];
for (int j = 2; j < N; ++j)
{
DP[0][j] = max(DP[1][j - 2], DP[1][j - 1]) + ST[0][j];
DP[1][j] = max(DP[0][j - 2], DP[0][j - 1]) + ST[1][j];
}
cout << max(DP[0][N - 1], DP[1][N - 1]) << '\n';
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
int T;
cin >> T;
for (int i = 0; i < T; ++i)
{
Test();
}
}
다이나믹 프로그래밍 문제입니다.
문제에서 주어지는 스티커 배치 정보가 가변 크기의 행렬로 주어지는데, 행의 개수는 2로 고정되어 있습니다.
따라서 0 번째 열부터 N - 1 번째 열까지 탐색하는 j 값을 증가시키면서
j 번째 열에 해당하는 각 스티커까지의 최대값을 DP 행렬에 저장하도록 해서 풀었습니다.
주어진 예시에서 DP[0][2]의 값을 구하려고 한다면,
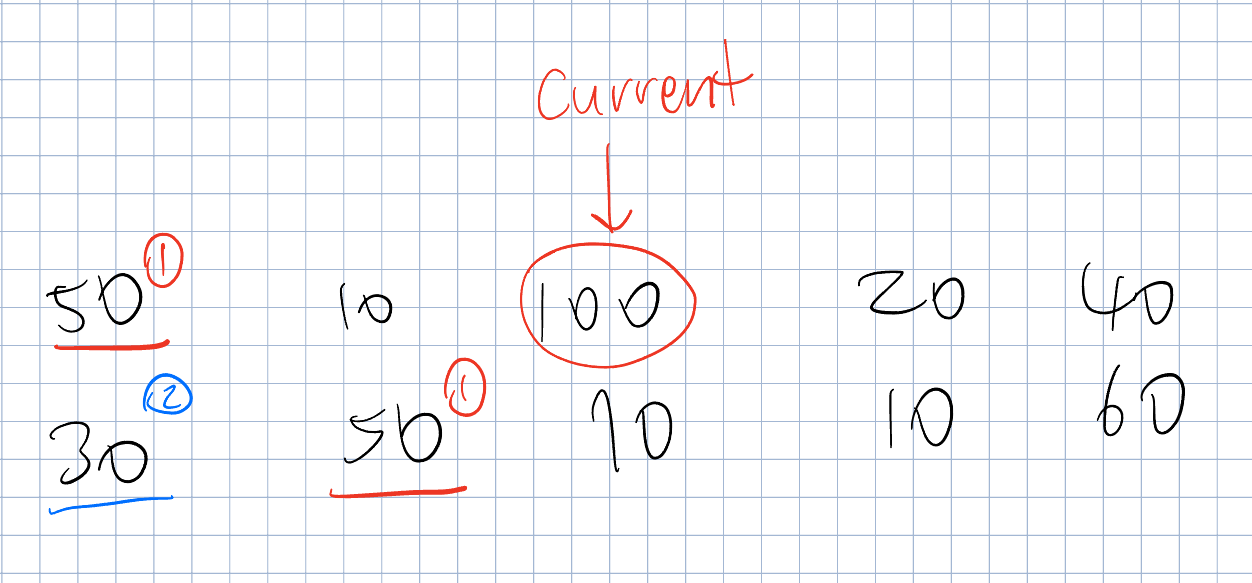
1번(50, 50) 스티커를 선택하는 경우와 2번(30) 스티커를 선택하는 경우 중 최대값을 골라야 합니다.
이를 일반화된 점화식으로 나타내면 다음과 같습니다.
DP[0][j] = max(DP[1][j - 2], DP[1][j - 1]) + ST[0][j]
1행 2열의 스티커의 경우도 마찬가지로
DP[1][j] = max(DP[0][j - 2], DP[0][j - 1]) + ST[1][j]
행의 값만 반대로 바꿔서 똑같이 나타낼 수 있습니다.
해당 점화식을 이용해서 DP 배열을 모두 채우고나면
마지막 열의 두 스티커 중 더 큰 값이 답이 됩니다.
'PS > 알고리즘 문제풀이' 카테고리의 다른 글
| [백준 C++] 18115 카드 놓기 - 덱 (0) | 2024.02.20 |
|---|---|
| [백준 C++] 11660 구간 합 구하기 5 - 다이나믹프로그래밍 (0) | 2024.02.20 |
| [백준 C++] 1932 정수 삼각형 - 다이나믹프로그래밍 (0) | 2024.02.20 |
| [백준 C++] 1629 곱셈 - 분할정복 (0) | 2024.02.20 |
| [백준 C++] 1149 RGB거리 - 다이나믹프로그래밍 (0) | 2024.02.20 |




